Quantum Tunneling : How does it work?
Quantum tunneling is a phenomenon in quantum mechanics that allows particles to pass through a potential energy barrier that they classically should not be able to overcome. This seemingly impossible feat arises from the wave-particle duality of matter, where particles can exhibit wave-like properties. Just as a wave can penetrate a barrier, a particle's wave function can have a non-zero probability of existing on the other side of a barrier, even if its energy is lower than the barrier's height.
Fundamentals of Quantum Tunneling
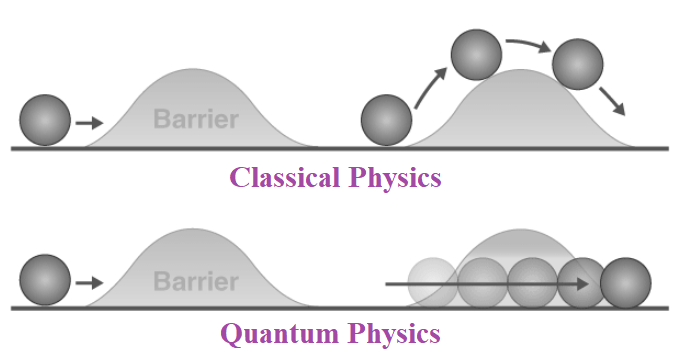
In classical physics, if a particle does not possess enough energy to surmount a barrier, it cannot pass through it. However, in quantum mechanics, particles exhibit both wave-like and particle-like properties, allowing for the possibility of "tunneling" through barriers.
Wavefunction
The wavefunction describes the quantum state of a particle. When a wavefunction encounters a potential barrier, part of it can penetrate through the barrier, despite the particle not having the energy to go over it.
Probability Amplitude
Quantum mechanics does not provide certainties but probabilities. The wavefunction's amplitude inside the barrier is non-zero, indicating a finite probability of the particle passing through the barrier.
The probability of tunneling depends on several factors, including the mass of the particle, the height and width of the barrier, and the particle's energy. Lighter particles, such as electrons, are more likely to tunnel through barriers than heavier ones. Similarly, thinner and lower barriers are more easily penetrated. The probability of tunneling decreases exponentially with the width and height of the barrier.
Quantum Tunneling Mechanism
Potential Barrier
A potential barrier is a region where the potential energy of a particle is higher than its kinetic energy. This could be represented as a hill or an obstacle in classical terms.Penetration through Barrier
When a particle encounters the barrier, the wavefunction does not immediately drop to zero at the barrier's edges. Instead, it gradually decreases exponentially within the barrier, suggesting a diminishing but non-zero probability of finding the particle inside the barrier.
Emergence on the Other Side
The particle can emerge on the other side of the barrier. This process is probabilistic, so not every particle will tunnel, but some will. The thicker or higher the barrier, the lower the probability of tunneling.
Applications of Quantum Tunneling
Quantum tunneling has several important applications in various fields:
- Nuclear Fusion: In stars, fusion reactions occur due to quantum tunneling, allowing atomic nuclei to overcome electrostatic repulsion and fuse, releasing energy.
- Semiconductors: Tunneling is vital in semiconductor technology. Tunneling diodes and field-effect transistors (FETs) utilize quantum tunneling for faster and more efficient electronic devices.
- Scanning Tunneling Microscope (STM): This device uses quantum tunneling to image surfaces at the atomic level. It operates by measuring the tunneling current between a sharp tip and the sample.
Tunneling in Quantum Computing
In quantum computing, tunneling plays a significant role in:
- Quantum Annealing: Used in optimization problems, quantum annealers like the D-Wave system rely on tunneling to reach the ground state of a system more efficiently.
- Error Correction: Understanding tunneling helps develop error-correcting codes and fault-tolerant quantum computing systems, as it can lead to decoherence and errors in quantum systems.
Conclusion
Quantum tunneling reveals the remarkable and counterintuitive nature of quantum mechanics, allowing particles to pass through barriers impossible in classical physics. Its principles are not only essential for understanding fundamental physics but also for practical technologies ranging from electronics to quantum computing.