Quantum Gates and Circuits
Quantum gates and circuits are the fundamental building blocks of quantum computation. Just as classical computers use logic gates like AND, OR, and NOT to manipulate bits of information, quantum computers use quantum gates to manipulate qubits.
Quantum Gates
Quantum gates are unitary operations that act on the state of a qubit or a system of qubits. They are represented mathematically by unitary matrices. Some of the most important quantum gates include:
Pauli Gates (X, Y, Z)
These are single-qubit gates that represent quantum analogs of classical NOT operations and rotations around different axes.
- X Gate:Also known as the quantum NOT gate, it flips the state of a qubit.
- Y Gate:Represents a rotation around the Y-axis.
- Z Gate:Represents a rotation around the Z-axis.
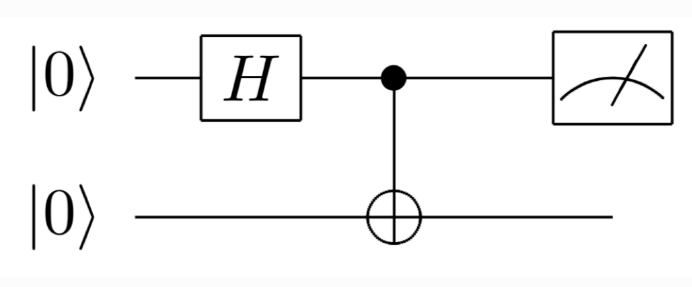
Hadamard Gate (H)
This gate creates superposition by transforming a qubit from a basis state (0 or 1) into an equal superposition of both states.
Phase Gate (S)
This gate applies a phase shift to the qubit.
CNOT Gate
A two-qubit gate that flips the second qubit (target) if the first qubit (control) is in the state 1. It's essential for creating entanglement between qubits.
Quantum Circuits
Quantum circuits are composed of sequences of quantum gates applied to qubits. They describe how quantum information is processed. In a quantum circuit, qubits are initialized in a specific state, quantum gates are applied to manipulate the qubits, and finally, measurements are performed to extract classical information from the quantum system.
A simple example of a quantum circuit could involve the following steps:
- Initialization:Set the qubits to a known state (usually |0>).
- Application of Quantum Gates:Apply a series of quantum gates to create superposition and entanglement.
- Measurement:Measure the final state of the qubits to obtain a classical result.
Why Quantum Gates and Circuits are Important
Quantum gates and circuits are the foundation of quantum computing. They enable the construction of algorithms that can solve certain problems much faster than classical algorithms. For example, Shor's algorithm for factoring large numbers and Grover's algorithm for searching unsorted databases are both implemented using quantum circuits.
The unique properties of quantum gates, such as superposition and entanglement, allow quantum computers to perform complex computations that are infeasible for classical computers. As research in quantum computing progresses, we expect to see more practical applications and advancements in this field.
Conclusion
Quantum gates and circuits are essential for understanding and developing quantum algorithms, which are algorithms that can be executed on a quantum computer. These algorithms have the potential to revolutionize many fields, including medicine, materials science, and cryptography.