Quantum Circuits
Quantum circuits are the backbone of quantum computing. They consist of sequences of quantum gates applied to qubits to perform quantum computations. Just like classical circuits process bits using classical gates, quantum circuits process qubits using quantum gates. The unique properties of qubits, such as superposition and entanglement, enable quantum circuits to perform complex computations that are infeasible for classical computers.

A quantum circuit is essentially a sequence of quantum gates applied to a system of qubits. These gates, such as the Hadamard gate, Pauli gates (X, Y, Z), CNOT gate, and others, manipulate the quantum state of the qubits. The order in which these gates are applied is crucial, as it determines the overall computation. Quantum circuits utilize the unique properties of quantum mechanics, such as superposition and entanglement, to perform computations that are beyond the reach of classical computers.
Quantum circuits are represented diagrammatically, with wires representing qubits and boxes representing quantum gates. The flow of the circuit is typically from left to right, indicating the order in which the gates are applied. Measurements can also be included in the circuit, which collapse the quantum state of the qubits to a classical state, allowing for the extraction of the computational result.
Constructing a Quantum Circuit
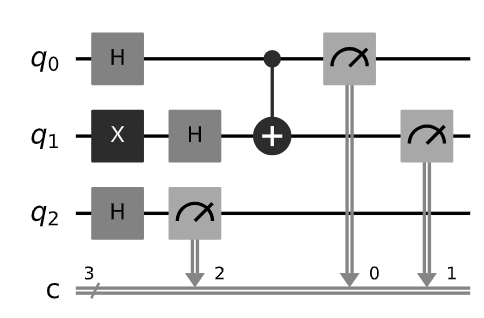
Constructing a quantum circuit involves the following steps:
- Initialization:Set the qubits to a known state, usually |0>.
- Application of Quantum Gates:Apply a sequence of quantum gates to manipulate the qubits. The choice and order of gates depend on the specific quantum algorithm being implemented.
- Measurement:Measure the qubits to obtain classical bits. The measurement outcome provides the result of the quantum computation.
Quantum Algorithms
Quantum circuits are used to implement quantum algorithms, such as:
- Shor's Algorithm:For factoring large integers exponentially faster than classical algorithms.
- Grover's Algorithm:For searching unsorted databases quadratically faster than classical algorithms.
These algorithms exploit the unique properties of quantum mechanics to solve problems more efficiently than classical algorithms.
Importance of Quantum Circuits
Quantum circuits enable the practical implementation of quantum algorithms, which have the potential to revolutionize fields such as cryptography, optimization, and drug discovery. As research in quantum computing progresses, quantum circuits will play a crucial role in developing new technologies and applications.
Conclusion
Quantum circuits have the potential to revolutionize various fields, including drug discovery, materials science, and cryptography. By leveraging the power of quantum mechanics, they can solve complex problems that are intractable for classical computers, opening up new frontiers in scientific research and technological innovation.