Single Qubit Gates | Quantum logic gate

Single-qubit gates are fundamental operations in quantum computing that act on a single qubit at a time. They manipulate the quantum state of the qubit, altering its properties and preparing it for further computations within a quantum circuit. These gates are analogous to basic logic gates like NOT, AND, and OR in classical computing, forming the building blocks for more complex quantum operations.

Mathematically, single-qubit gates are represented by 2x2 unitary matrices. Unitary matrices ensure that the quantum state remains normalized after the gate operation, preserving the probabilistic nature of quantum mechanics. Some of the most important single-qubit gates include:

Identity Gate (I)

The Identity Gate (I) in quantum computing is essentially a "do-nothing" operation. It has no effect on the qubit it's applied to.

Key Characteristics:

1. Placeholder:It can be used as a placeholder in quantum circuits, especially when designing or analyzing more complex circuits.
2. Error Correction:In some error correction schemes, the Identity Gate can be used to simulate the effect of no error occurring on a qubit.
3. Circuit Analysis:It's useful in mathematical proofs and circuit analysis for understanding the overall behavior of a quantum circuit.

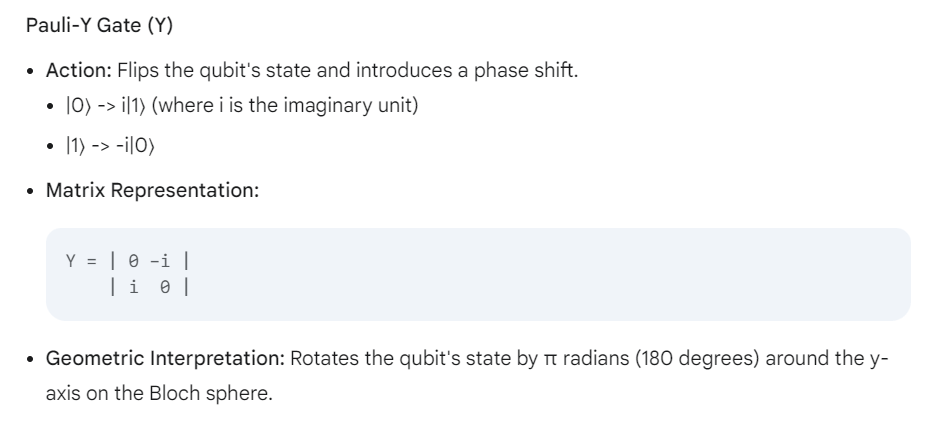
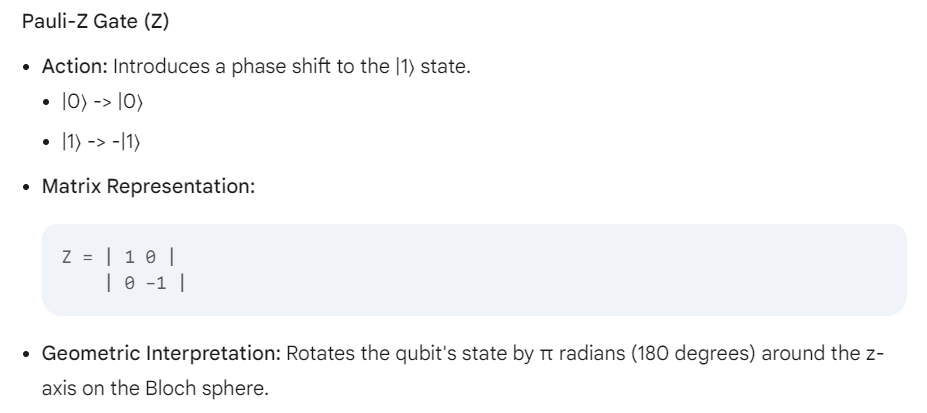
Pauli Gates (X, Y, Z)

The Pauli gates (X, Y, and Z) are fundamental single-qubit operations in quantum computing. They represent rotations around the x, y, and z axes of the Bloch sphere, a geometric representation of the qubit's possible states.

Hadamard Gate (H)

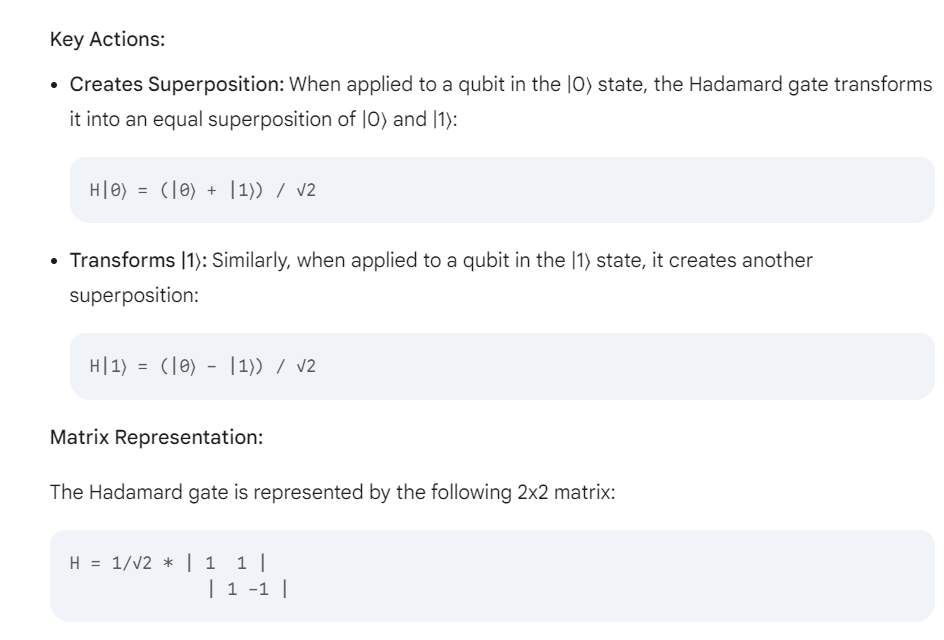
The Hadamard gate (H) is a crucial single-qubit gate in quantum computing. It's renowned for its ability to create superposition states, a fundamental concept in quantum mechanics that allows quantum computers to explore multiple possibilities simultaneously.

Geometric Interpretation:

On the Bloch sphere, the Hadamard gate performs a rotation of 180 degrees around the axis that lies halfway between the x-axis and the y-axis. This rotation effectively moves the qubit from the 0? state (north pole) to the equator of the Bloch sphere, creating a superposition.

Significance:

1. Superposition:The Hadamard gate is essential for creating superposition states, which are the foundation of quantum algorithms like Grover's search algorithm and Shor's algorithm.
2. Basis Change:It can be seen as a change of basis, transforming the computational basis states (|0> and |1>) into a different basis known as the Hadamard basis.
3. Universality:Although not universal on its own, the Hadamard gate, combined with other single-qubit gates like the Pauli-X gate, forms a universal set of gates, meaning any single-qubit operation can be approximated to arbitrary accuracy using combinations of these gates.

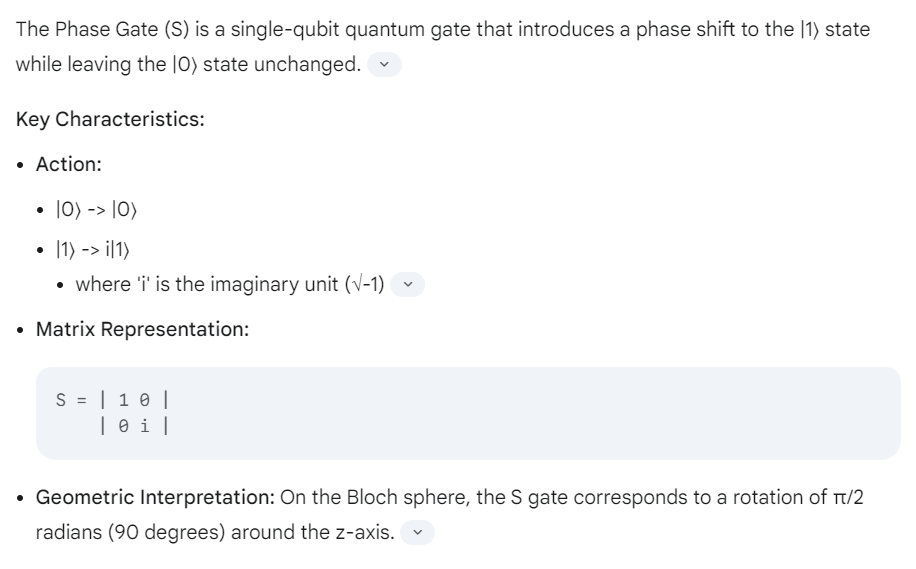
Phase Gate (S)

Significance:

1. Phase Manipulation:The S gate is crucial for manipulating the phase of a qubit, a critical aspect of many quantum algorithms.
2. Building Block:It's a fundamental building block for other quantum gates, such as the T gate (p/4 phase shift).
3. Universal Gate Sets:Although not universal on its own, the S gate, in combination with other gates like the Hadamard gate and the Pauli-X gate, forms a universal set of gates for quantum computation.

T Gate

Visualizing Single-Qubit Gates on the Bloch Sphere

The Bloch sphere is a useful representation of a qubit's state. A single-qubit gate can be visualized as a rotation on this sphere.

1. X Gate:Rotates the qubit state 180 degrees around the X-axis.
2. Y Gate:Rotates the qubit state 180 degrees around the Y-axis.
3. Z Gate:Rotates the qubit state 180 degrees around the Z-axis.
4. Hadamard Gate:Puts the qubit into a superposition by rotating it around an axis that lies between the X and Z axes.

Importance of Single-Qubit Gates

Single-qubit gates are crucial for quantum computing because they allow precise control over the state of each qubit. They are the building blocks for more complex quantum operations and algorithms. By combining single-qubit gates with multi-qubit gates (like the CNOT gate), we can construct any quantum circuit.

Conclusion

By combining these and other single-qubit gates, quantum computers can perform a wide range of operations, manipulating the qubits' states in intricate ways to solve complex problems that are intractable for classical computers.