Quantum States and Qubits
Quantum states are the fundamental building blocks of quantum systems. They represent the possible configurations or conditions that a quantum system can be in. Unlike classical systems, which exist in definite states, quantum systems can exist in a superposition of multiple states simultaneously. This means that a quantum system is not in any one specific state but rather in a combination of all possible states, each with a certain probability.
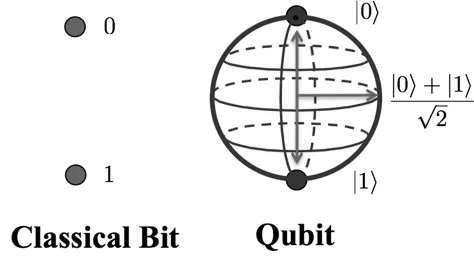
Qubits, or quantum bits, are the basic units of quantum information. They are analogous to classical bits, which are the fundamental units of classical information and can take on the values of 0 or 1. However, unlike classical bits, qubits can exist in a superposition of both 0 and 1 simultaneously. This unique property of qubits allows quantum computers to perform.
Quantum States
Quantum states describe the condition or configuration of a quantum system. Unlike classical states, which are deterministic and distinct, quantum states can exist in superpositions, representing multiple possibilities at once. Here's a detailed look at quantum states:
Wave Function
A quantum state is mathematically represented by a wave function. The wave function contains all the information about the system's probabilities. For example, an electron's position and momentum.
Probability Amplitude
The wave function's values are complex numbers, and their squared magnitudes represent the probabilities of the system being in different states. This probabilistic nature is a key feature of quantum mechanics.
Superposition
A quantum system can be in a superposition of states, meaning it can exist in multiple states simultaneously. When measured, the superposition collapses into one of the possible states.
Eigenstates and Eigenvalues
When a measurement is made, a quantum system collapses into one of its eigenstates, and the corresponding measurement result is an eigenvalue. For example, the spin of an electron can be measured as up or down, which are the eigenstates.
Qubits
A qubit, or quantum bit, is the fundamental unit of information in quantum computing. It is analogous to a classical bit but with unique quantum mechanical properties. Here's an in-depth exploration of qubits:
Quantum Superposition
Unlike a classical bit that can be either 0 or 1, a qubit can be in a superposition of both 0 and 1.
Quantum Entanglement
Qubits can be entangled with each other, creating a shared state where the state of one qubit is dependent on the state of another. This entanglement is crucial for quantum computing, allowing for complex correlations and faster computations.
Quantum Interference
The probability amplitudes of qubits can interfere with each other, enabling the construction of quantum algorithms that can solve certain problems more efficiently than classical algorithms.
Bloch Sphere Representation
A qubit's state can be visualized on the Bloch sphere, a 3D representation where any point on the surface corresponds to a possible state of the qubit. The poles of the sphere represent the basis states 0> and 1>, and any point on the sphere represents a superposition of these states.
Quantum Gates and Quantum Circuits
Quantum Gates
Quantum gates are the building blocks of quantum circuits, analogous to classical logic gates but operating on qubits. They manipulate qubits by performing unitary transformations, preserving the quantum nature of the states. Common quantum gates include the Pauli-X, Y, Z gates, and more complex gates like the Hadamard (H) and Controlled-NOT (CNOT) gates.
Quantum Circuits
Quantum computation is performed by applying a sequence of quantum gates to a set of qubits. Quantum circuits are used to implement quantum algorithms, which exploit superposition and entanglement to solve problems more efficiently than classical algorithms.
Applications of Qubits
- Quantum Computing: Qubits and quantum gates form the basis of quantum computers, which can solve specific problems, such as factoring large numbers and simulating quantum systems, faster than classical computers.
- Quantum Cryptography: Qubits are used in quantum key distribution (QKD) to create secure communication protocols, exploiting the principles of superposition and entanglement to ensure security.
- Quantum Sensing and Imaging: Qubits are leveraged in advanced sensing and imaging technologies, providing high precision and sensitivity for applications including medical diagnostics and environmental monitoring.
Conclusion
Quantum states and qubits are foundational concepts in quantum mechanics and quantum computing, representing the complex and fascinating behavior of particles at the quantum level. These principles enable the development of powerful quantum technologies, from secure communication systems to advanced computing and sensing applications. Understanding quantum states and qubits is essential for exploring the cutting-edge advancements in quantum science and technology.