Correlation in Machine Learning
Correlation stands as a fundamental statistical concept that portrays the relationship between two variables. It offers crucial insights into how changes in one variable correspond to changes in another. This relationship can be utilized to predict or infer one quantity based on the knowledge of the other.
Positive Correlation
Positive Correlation denotes a scenario where as the value of one variable increases, the value of the other variable also increases. This positive association implies that the two variables move in tandem, rising or falling together. It signifies a direct and proportional connection between the variables.
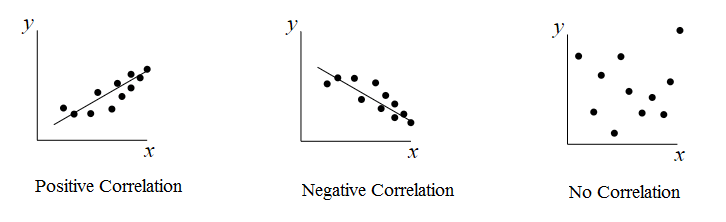
Negative Correlation
Negative Correlation describes a situation where an increase in one variable leads to a decrease in the other variable. In this case, the two variables move in opposite directions. As one variable increases, the other decreases, and vice versa. This inverse relationship showcases an indirect and inversely proportional connection.
No Correlation
No Correlation signifies a lack of discernible relationship between the variables. When the values of one variable increase or decrease, there is no apparent impact on the values of the other variable(s). In such instances, the variables appear to be unrelated, and their changes do not influence each other.
You can plot correlation matrix to show which variable is having a high or low correlation in respect to another variable.
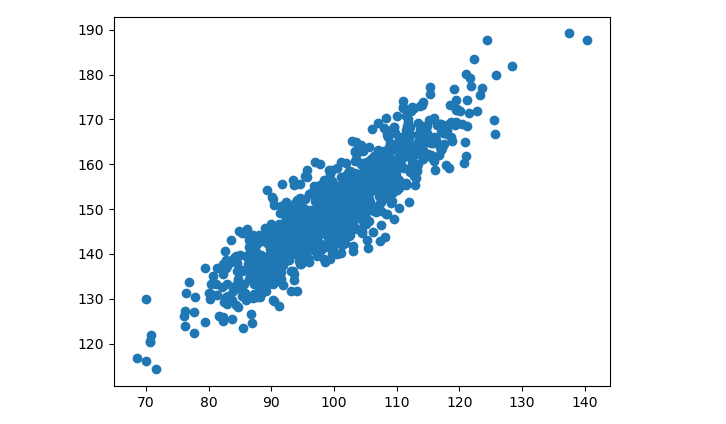
Above code will generate a scatter plot of the two variables (var1, var2) and there is a relationship between the two variables of increasing trend.
Correlation coefficients, such as Pearson's correlation coefficient or Spearman's rank correlation coefficient, are commonly used to quantify the strength and direction of the correlation between variables. These coefficients provide a numerical measure of the degree of association, allowing researchers to ascertain the intensity of the relationship between the variables.
Conclusion
Understanding correlation is vital in various fields, including finance, economics, social sciences, and natural sciences, as it aids in predicting outcomes, identifying patterns, and making informed decisions based on the relationships between variables.