Standard Deviation - Machine Learning
Variance serves as a measure of the dispersion or spread of data within a dataset. It quantifies the average of the squared differences between each data point and the mean of the dataset. By squaring the differences, the variance accentuates the relative significance of deviations from the mean, thereby capturing the overall variability in the data.
To calculate the variance, one sums up the squared differences between each data point and the mean, then divides the sum by the total number of data points. The result offers a numeric representation of the average dispersion of data points around the mean, enabling analysts to assess the extent to which data is spread across the dataset.
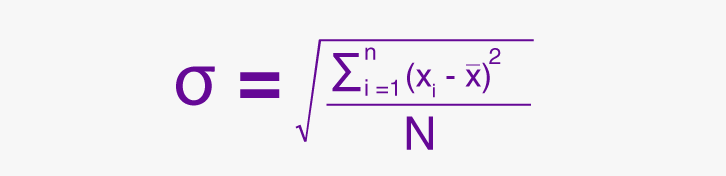
Standard Deviation, often abbreviated as "std," arises as an inherent companion to the variance. It provides a concise numerical description of how spread out the values are in a dataset, particularly concerning their proximity to the mean. As an intuitive and widely-used measure, the standard deviation conveys the extent to which data points deviate from the mean, thereby revealing the distribution's overall variability.
How to find the Standard Deviation of a dataset
The standard deviation can be used to identify outliers in your data. If a value is a certain number of Standard Deviation away from the mean, that data point is identified as an outlier.
A low standard deviation implies that the majority of data points cluster closely around the mean, signifying a more concentrated distribution. Conversely, a high standard deviation indicates that the data points are more dispersed and span a wider range from the mean, characterizing a more scattered distribution.
How to find outliers?
Z-scores can quantify the unusualness of an observation when your data follow the normal distribution . The following code calculate the cut-off for identifying outliers as more than 3 standard deviations from the mean.
Next step is to identify outliers that fall outside of the defined lower and upper limits.
Alternately, you can filter out those values from the sample that are not within the defined limits.
Conclusion
Both the variance and the standard deviation offer valuable insights into the dispersion and variability present in the dataset, enabling researchers, analysts, and decision-makers to comprehend the extent of spread within the data. They continue to be vital tools in statistical analysis, enriching our understanding of datasets and paving the way for informed interpretations and conclusions.