Python - Mean(), Median(), Mode()

By: Rajesh P.S.

Central Tendency serves as a crucial concept, representing a central or prototypical value within a probability distribution. This fundamental notion enables analysts to identify the core, average, or most frequently occurring value in a given dataset. Measures of central tendency, therefore, play an essential role in unraveling the essence of a dataset and understanding its central characteristics.

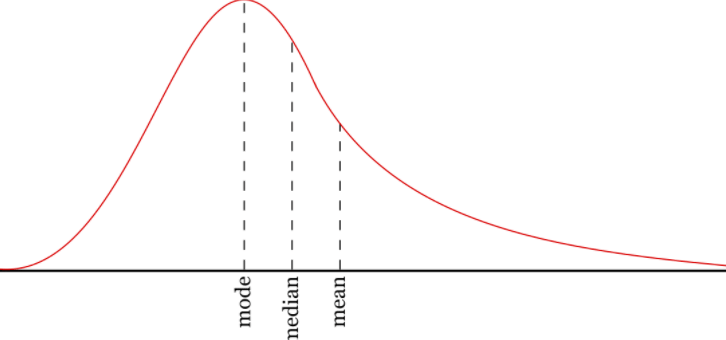
Mean : The mean value is the average value.
Median : The median value is the value in the middle, after you have sorted all the values.
Mode : The Mode value is the value that appears the most number of times.

Find the mean, median and mode from a Pandas column using Python

Continue Reading...

Lets create a DataFrame...

df = pd.DataFrame([[32, 24, 30, 40], [17, 24, 21, 28], [50, 25, 28, 32], [25, 34, 21, 48], [17, 31, 18, 28], [35, 24, 19, 42]], columns=['Physics', 'Chemistry', 'Biology', 'Maths'], index=['Student-1', 'Student-2', 'Student-3', 'Student-4', 'Student-5', 'Student-6'])

Physics Chemistry Biology Maths Student-1 32 24 30 40 Student-2 17 24 21 28 Student-3 50 25 28 32 Student-4 25 34 21 48 Student-5 17 31 18 28 Student-6 35 24 19 42

Calculate Mean

The Mean stands out as one of the most prevalent measures of central tendency. Calculated as the sum of all data points divided by the total number of observations, the Mean presents a comprehensive overview of the data's average value. Its mathematical elegance and simplicity make it a widely favored tool for capturing the typical magnitude of a dataset.

df.mean()

Physics 29.333333 Chemistry 27.000000 Biology 22.833333 Maths 36.333333

If you want to find out the mean of a single column in a DataFrame:

df['column_name'].mean()

df['Chemistry'].mean()

27.0

By default, mean is calculated every single column (axis=0) in the DataFrame. If you Pass the argument of (axis=1) will return the mean of every single row in the DataFrame .

df.mean(axis=1)

Student-1 31.50 Student-2 22.50 Student-3 33.75 Student-4 32.00 Student-5 23.50 Student-6 30.00

Calculate Median

The Median is the middle value when the dataset is ordered from the smallest to the largest (or vice versa). Unlike the Mean, the Median is less affected by extreme outliers, making it a robust representation of the central value, particularly in datasets with skewed distributions.

df.median()

Physics 28.5 Chemistry 24.5 Biology 21.0 Maths 36.0

If you want to find out the median of a single column in a DataFrame:

df['column_name'].median()

df['Chemistry'].median()

24.5

By default, median is calculated every single column (axis=0) in the DataFrame. If you Pass the argument of (axis=1) will return the median of every single row in the DataFrame .

df.median(axis=1)

Student-1 31.0 Student-2 22.5 Student-3 30.0 Student-4 29.5 Student-5 23.0 Student-6 29.5

Calculate Mode

The Mode deserves special mention as yet another essential measure of central tendency. The Mode refers to the value that appears most frequently within the dataset. It stands as a valuable indicator of the most prevalent occurrence, providing insights into the dominant characteristic of the data.

df.mode()

Physics Chemistry Biology Maths 0 17 24 21 28

Summary Statistics

This function gives you several useful things all at the same time.

df.describe()

Physics Chemistry Biology Maths count 6.000000 6.00000 6.000000 6.000000 mean 29.333333 27.00000 22.833333 36.333333 std 12.564500 4.38178 4.956477 8.238123 min 17.000000 24.00000 18.000000 28.000000 25% 19.000000 24.00000 19.500000 29.000000 50% 28.500000 24.50000 21.000000 36.000000 75% 34.250000 29.50000 26.250000 41.500000 max 50.000000 34.00000 30.000000 48.000000

Conclusion

Using these measures of central tendency, analysts can discern the core characteristics of a dataset, thereby illuminating critical patterns and trends. Understanding the central tendencies of data is a foundational step in statistical analysis, paving the way for further exploration and decision-making processes across various fields, including finance, economics, social sciences, and more.

Next > How to find Inter-Quartile Range (IQR)

Related Topics

More Related Topics.....