Multiple Linear Regression | Python

Multiple Linear Regression (MLR) is an extension of Simple Linear Regression (SLR), used to assess the association between two or more explanatory variable(s) and a single response variable. In Simple Linear Regression you use a single independent (explanatory) variable to predict the value of a dependent (response) variable. With Simple Linear Regression model your data as follows: y(pred) = b0 + b1 * x This is a line where y(pred) is the output variable you want to predict, x is the input variable and b0 and b1 are coefficients that you need to estimate that move the line around.

Multiple Linear Regression

Multiple Linear Regression determines the relationship between one dependent variable and a set of independent variable(s) .

Let's take an example:

Imagine that you are a tourist guide. You need to provide the price range of food to your clients. The price of those food usually correlates with the Food Quality and Service Quality of the Restaurant. The bigger they are, the more expensive the food was.

Above example explains a linear relationship exists when increasing or decreasing the independent variable(s) results in a corresponding increase or decrease of the dependent variable. In Multiple Linear Regression , with 'n' predictor variables (x), the prediction of y(pred) is expressed by the following equation: y(pred) = b0 + b1x1 + b2x2 + .... + bn * xn Here, y(pred) is the variable that you are trying to predict, x's are the variables that you are using to predict y(pred), b0 is the intercept, and b's are the regression coefficients.

Multiple linear regression Example:

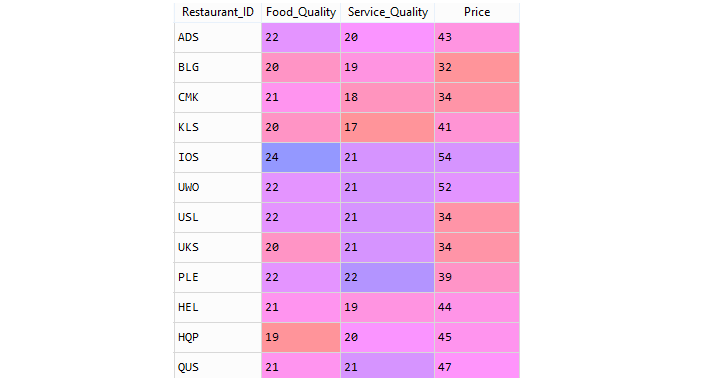
Consider the Restaurant data set: restaurants.csv . A restaurant guide collects several variables from a group of restaurants in a city. The description of the variables is given below:
Field Description
Restaurant_ID Restaurant Code
Food_Quality Measure of Quality Food in points
Service_Quality Measure of quality of Service in points
Price Price of meal

Restaurant data sample,

What is Multiple Linear Regression? - Python

Loading required Python packages

import pandas from sklearn import linear_model

Importing dataset

The Python Pandas module allows you to read csv files (read_csv()) and return a DataFrame object . The file is meant for testing purposes only, you can download it from here: restaurants.csv .
df = pandas.read_csv("restaurants.csv")
Identifying the dependent(y) and independent variables(X) .
X = df[['Food_Quality', 'Service_Quality']] y = df['Price']

Define the Model

Next step is to define the Linear Regression model . So, you have a variable named "regr" and assign it an instance of the Linear Regression class imported from sklearn.
regr = linear_model.LinearRegression()

Fit the Model

The "regr" object has a method called fit() that takes the independent(X) and dependent(y) values as arguments and fills the regression object with data that describes the relationship:
regr.fit(X, y)

Predict

Now you have a regression object that are ready to predict Food Price based on a Restaurant's Food_Quality and Service_Quality . So, next step is to predict the Food Price of a Restaurant where Food_Quality 25 points and Service Quality is 22 points.
#predict price where Food_Quality is 25 and Service_Quality is 22 predictedPrice = regr.predict([[25, 22]])

Full Source | Python

import pandas from sklearn import linear_model df = pandas.read_csv("restaurants.csv") X = df[['Food_Quality', 'Service_Quality']] y = df['Price'] regr = linear_model.LinearRegression() regr.fit(X, y) predictedPrice = regr.predict([[25, 22]]) print("Predicted Food Price" , predictedPrice)
Predicted Food Price [56.95600559]

Above result shows that a Restaurant with Food Quality 25 points and Service qulity 22 points, will charge the Food price 56.956.

Coefficient

The Coefficient is a factor that describes the relationship with an unknown variable.

For example: if x is a variable, then 2x is x two times. x is the unknown variable, and the number 2 is the coefficient.

Next step is to find out the coefficient value of Food_Quality against Price, and for Service_Quality against Price. The Results you get explain what would happen if you increase, or decrease, one of the independent values. Find the Coefficient values of the regression object:
import pandas from sklearn import linear_model df = pandas.read_csv("restaurants.csv") X = df[['Food_Quality', 'Service_Quality']] y = df['Price'] regr = linear_model.LinearRegression() regr.fit(X, y) print("Coefficient Values : " , regr.coef_)
Coefficient Values : [3.02723464 0.26606145]
The result values represents the Coefficient values of Food_Quality and Service_Quality.
  1. Food_Quality : 3.02723464
  2. Service_Quality : 0.26606145
Above coefficient values explains that if the Food_Quality increase by 1 point, the Price increases by 3.02723464. Also if the Service_Quality increases by 1 point, the Price emission increases by 0.26606145. So, let's test it now!

You have already predicted that if Food_Quality with a 25 points and Service_Quality with a 22 points, the Price will be approximately 56.956.

Now, you can test it if you increase the Food_Quality with 10 points (25+10 = 35).

import pandas from sklearn import linear_model df = pandas.read_csv("restaurants.csv") X = df[['Food_Quality', 'Service_Quality']] y = df['Price'] regr = linear_model.LinearRegression() regr.fit(X, y) predictedPrice = regr.predict([[35, 22]]) print("Predicted Food Price" , predictedPrice)
Predicted Food Price [87.22835196]

The above code predicted that a Restaurant with Food_Quality 35 points and Service_Quality with 22 points will charge the Food Price approximately 87.228.

Which shows that the Coefficient of 3.02723464 is correct: 56.95600559 + (10 * 3.02723464) = 87.2283

Where,

  1. 56.95600559 is the Predicted Food Price when Food_Quality 25 points.
  2. 10 is the increased Food_Quality points.
  3. 3.02723464 is the Coefficient Value of Food_Quality.





Related Topics
  1. Simple Linear Regression | Python Data Science
  2. Ordinary Least Squares Regression | Python Data Science
  3. Polynomial Regression | Python
  4. Logistic Regression | Python Machine Learning
  5. K-Nearest Neighbor(KNN) | Python Machine Learning
  6. Decision Tree in Machine Learning | Python
  7. Random Forest | Python Machine Learning
  8. Support Vector Machine | Python Machine Learning