Polynomial Regression | Python Machine Learning

Regression is a powerful statistical method used to establish relationships between the independent variables (inputs used for prediction) and the dependent variable (the variable being predicted) to make outcome predictions.

When the data points do not follow a linear pattern, Polynomial Regression is a suitable alternative. It allows for modeling relationships that are not linear by using higher-order polynomials, enabling the prediction of outcomes with more complex curves. This flexibility makes Polynomial Regression a valuable tool in situations where linear relationships do not adequately capture the underlying data patterns.

The equation of the Polynomial Regression having an nth degree can be written as:

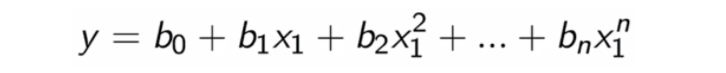
regression nth degree

Polynomial Regression example | Python

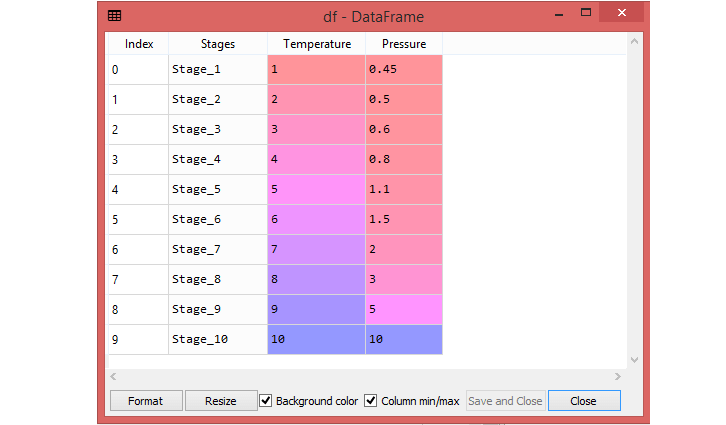
Here, some data of Pressure and Temperature related to each stages. So, using Polynomial Regression , check whether the data is showing the True or False in each stage. By checking the data available, found that there is a non-linear relationship between the Pressure and the Temperature. So, the goal is to build a Truth detector regression model using Polynomial Regression. Below are the steps to build such a model.


Python Machine Learning Polynomial Regression

Import the Python libraries

import numpy as nm import matplotlib.pyplot as mtp import pandas as pd

Define dataset

df = pd.DataFrame({"Stages" : (["Stage_1", "Stage_2", "Stage_3", "Stage_4", "Stage_5", "Stage_6", "Stage_7","Stage_8","Stage_9", "Stage_10" ]), "Temperature": ([1,2,3,4,5,6,7,8,9,10]), "Pressure":[0.45,0.5,0.6,0.8,1.1,1.5,2,3,5,10]})

Extracted the dependent(y) and independent variable(x) from the dataset.

x = df[['Temperature']] y = df['Pressure']

The dataset contains three columns (Stages, Temperature, and Pressure), but, here consider only two columns (Temperature and Pressure). In the following Polynomial Regression model , predict the output for Temperature 6.5 somewhere between stage_6 and stage_7.

In building Polynomial Regression, it is better to take the Linear regression model as reference and compare both the output.

Building the Linear regression model

linear_regs= LinearRegression() linear_regs.fit(x,y)

Above code create a Simple Linear model using linear_regs object of LinearRegression class and fitted it to the dataset variables (x and y).

Building the Polynomial regression model

polynomial_regs= PolynomialFeatures(degree= 2) x_poly= polynomial_regs.fit_transform(x)

Above code used polynomial_regs.fit_transform(x) , because first it convert your feature matrix into polynomial feature matrix, and then fitting it to the Polynomial regression model. The argument (degree= 2) depends on your choice. You can choose it according to our Polynomial features .

After executing the code, you will get another matrix x_poly, which you can be seen under the Spyder variable explorer:


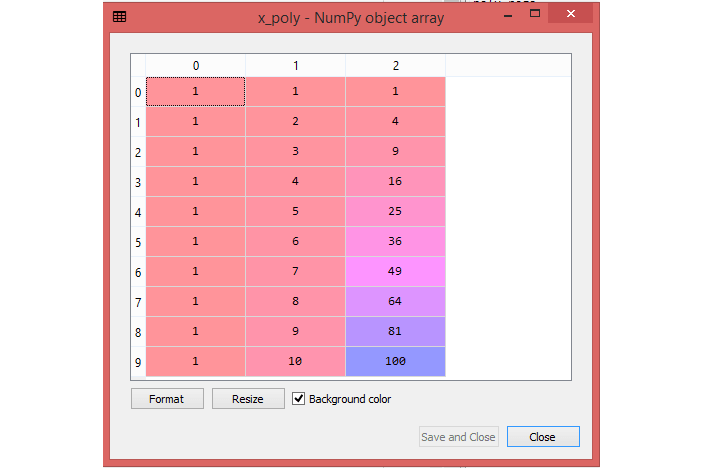
Machine Learning Basics: Polynomial Regression

Next step is to use another LinearRegression object , namely linear_reg_2, to fit your x_poly vector to the linear model.

linear_reg_2 =LinearRegression() linear_reg_2.fit(x_poly, y)

Linear regression Plot

Visualize the result for Linear regression model as you did in Simple Linear Regression.

mpl.scatter(x,y,color="blue") mpl.plot(x,linear_regs.predict(x), color="red") mpl.title("Truth detection model(Linear Regression)") mpl.xlabel("Temperature") mpl.ylabel("Pressure") mpl.show()
output:
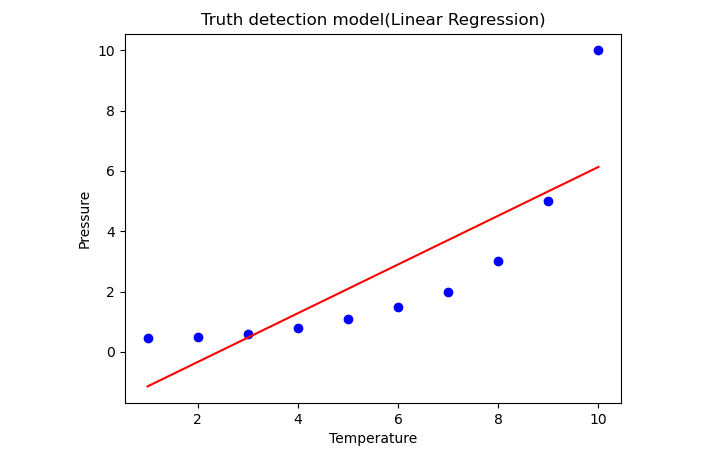
Implementation of Polynomial Regression in Python

Here, you can see that the regression line is so far from the datasets. Actual values in blue data points and Predictions are in a red straight line. If you consider this output to predict the value of Temperature, in some cases which is far away from the real value.

So, you need a curved model to fit the dataset other than a straight line.

Polynomial Regression Plot

mpl.scatter(x,y,color="blue") mpl.plot(x, linear_reg_2.predict(polynomial_regs.fit_transform(x)), color="red") mpl.title("Truth detection model(Polynomial Regression)") mpl.xlabel("Temperature") mpl.ylabel("Pressure") mpl.show()

Here, you have taken linear_reg_2.predict(poly_regs.fit_transform(x), instead of x_poly, because you want a Linear regressor object to predict the polynomial features matrix .


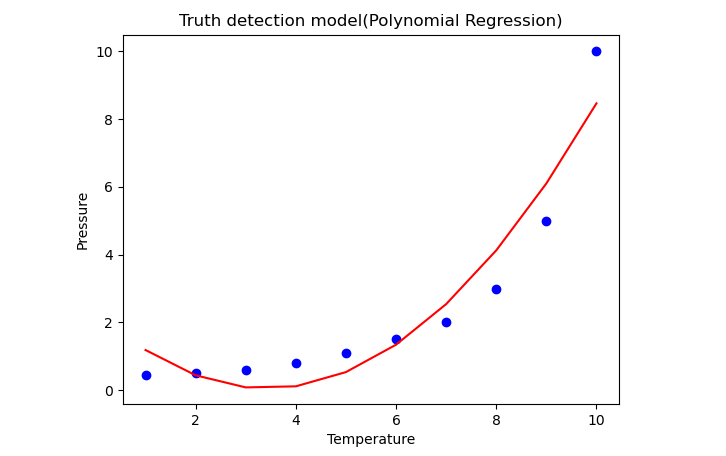
Polynomial Feature Transforms for Machine Learning

In the above image you can see the predictions are close to the real values. The above plot will vary as you will change the degree.

Change degree= 3

polynomial_regs= PolynomialFeatures(degree= 3)
output:
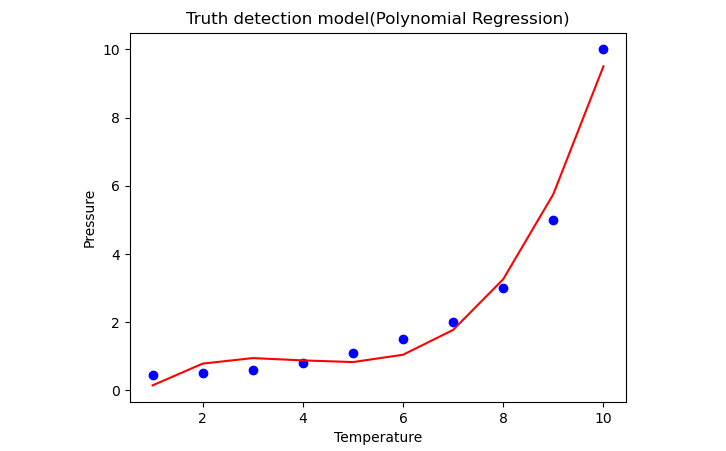
Python MACHINE LEARNING APPROACH TO POLYNOMIAL REGRESSION

Above image will give you a more accurate plot when you change the degree=3.

Change degree= 4

polynomial_regs= PolynomialFeatures(degree= 4)
output:
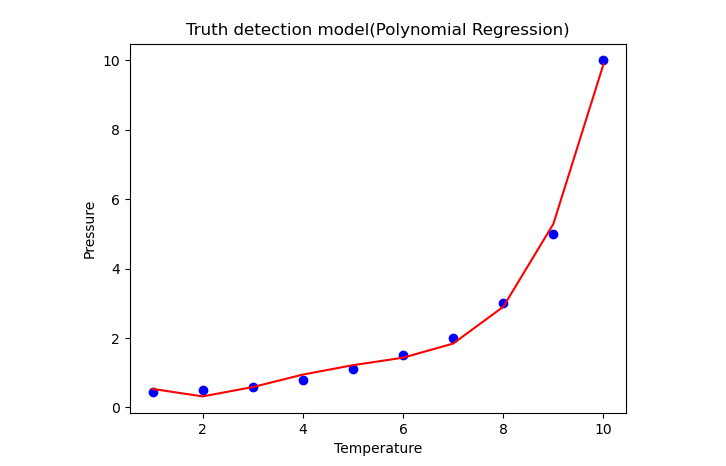
Linear Regression model

Above image will give you a most accurate plot. So, you will get more accurate results by increasing the degree of Polynomial.

Predicting the final result

Next step is to predict the final output using the models to see whether the data is true or false.

Linear Regression model

Here use the predict() method and will pass the value 6.5.

lin_pred = linear_regs.predict([[6.5]]) print("Linear Regression model Prediction : " , lin_pred)
Linear Regression model Prediction : [3.30378788]

Polynomial Regression model

Here also use the predict() method and will pass the value 6.5.

poly_pred = linear_reg_2.predict(polynomial_regs.fit_transform([[6.5]])) print("Polynomial Regression model Prediction : ", poly_pred)
Polynomial Regression model Prediction : [1.58862453]

Above code confirms that the predicted output for the Polynomial Regression is [1.58862453], which is much closer to real value.

Full Source | Python
import numpy as nm import pandas as pd from sklearn.linear_model import LinearRegression from sklearn.preprocessing import PolynomialFeatures import matplotlib.pyplot as mpl df = pd.DataFrame({"Stages" : (["Stage_1", "Stage_2", "Stage_3", "Stage_4", "Stage_5", "Stage_6", "Stage_7", "Stage_8", "Stage_9", "Stage_10" ]), "Temperature": ([1,2,3,4,5,6,7,8,9,10]), "Pressure":[0.45,0.5,0.6,0.8,1.1,1.5,2,3,5,10]}) x = df[['Temperature']] y = df['Pressure'] linear_regs= LinearRegression() linear_regs.fit(x,y) polynomial_regs= PolynomialFeatures(degree= 4) x_poly= polynomial_regs.fit_transform(x) linear_reg_2 =LinearRegression() linear_reg_2.fit(x_poly, y) mpl.scatter(x,y,color="blue") mpl.plot(x,linear_regs.predict(x), color="red") mpl.title("Truth detection model(Linear Regression)") mpl.xlabel("Temperature") mpl.ylabel("Pressure") mpl.show() mpl.scatter(x,y,color="blue") mpl.plot(x, linear_reg_2.predict(polynomial_regs.fit_transform(x)), color="red") mpl.title("Truth detection model(Polynomial Regression)") mpl.xlabel("Temperature") mpl.ylabel("Pressure") mpl.show() lin_pred = linear_regs.predict([[6.5]]) print("Linear Regression model Prediction : " , lin_pred) poly_pred = linear_reg_2.predict(polynomial_regs.fit_transform([[6.5]])) print("Polynomial Regression model Prediction : ", poly_pred)
output:
Linear Regression model Prediction : [3.30378788] Polynomial Regression model Prediction : [1.89498106]

Conclusion

Polynomial Regression is a type of regression analysis that extends the concept of linear regression to model non-linear relationships between independent and dependent variables. It utilizes higher-order polynomial functions to capture more complex patterns in the data, making it a valuable technique when linear regression is insufficient to represent the underlying relationship between variables.






Related Topics
  1. Simple Linear Regression | Python Data Science
  2. Multiple Linear Regression | Python Data Science
  3. Ordinary Least Squares Regression | Python Data Science
  4. Logistic Regression | Python Machine Learning
  1. K-Nearest Neighbor(KNN) | Python Machine Learning
  2. Decision Tree in Machine Learning | Python
  3. Random Forest | Python Machine Learning
  4. Support Vector Machine | Python Machine Learning